First-Principles AI finds crystallization of fractional quantum Hall liquids

When does a fractional quantum Hall (FQH) liquid crystallize? Addressing this question requires a framework that treats fractionalization and crystallization on equal footing, especially in strong Landau-level mixing regime. Here, we introduce MagNet, a self-attention neural-network variational wavefunction designed for quantum systems in magnetic fields on the torus geometry. We show that MagNet provides a unifying and expressive ansatz capable of describing both FQH states and electron crystals within the same architecture. Trained solely by energy minimization of the microscopic Hamiltonian, MagNet discovers topological liquid and electron crystal ground states across a broad range of Landau-level mixing. Our results highlight the power of first-principles AI for solving strongly interacting many-body problems and finding competing phases without external training data or physics pre-knowledge.

Is attention all you need to solve the correlated electron problem?

The attention mechanism has transformed artificial intelligence research by its ability to learn relations between objects. In this work, we explore how a many-body wavefunction ansatz constructed from a large-parameter self-attention neural network can be used to solve the interacting electron problem in solids. By a systematic neural-network variational Monte Carlo study on a moir\'e quantum material, we demonstrate that the self-attention ansatz provides an accurate, efficient, and unbiased solution. Moreover, our numerical study finds that the required number of variational parameters scales roughly as $N^2$ with the number of electrons, which opens a path towards efficient large-scale simulations.

Pairing-based graph neural network for simulating quantum materials

We develop a pairing-based graph neural network for simulating quantum many-body systems. Our architecture augments a BCS-type geminal wavefunction with a generalized pair amplitude parameterized by a graph neural network. Variational Monte Carlo with our neural network simultaneously provides an accurate, flexible, and scalable method for simulating many-electron systems. We apply this method to two-dimensional semiconductor electron-hole bilayers and obtain accurate results on a variety of interaction-induced phases, including the exciton Bose-Einstein condensate, electron-hole superconductor, and bilayer Wigner crystal. Our study demonstrates the potential of physically-motivated neural network wavefunctions for quantum materials simulations.

Artificial intelligence for artificial materials: moiré atom

Moir\'e engineering in atomically thin van der Waals heterostructures creates artificial quantum materials with designer properties. We solve the many-body problem of interacting electrons confined to a moir\'e superlattice potential minimum (the moir\'e atom) using a 2D fermionic neural network. We show that strong Coulomb interactions in combination with the anisotropic moir\'e potential lead to striking ``Wigner molecule" charge density distributions observable with scanning tunneling microscopy.

Topogivity: A Machine-Learned Chemical Rule for Discovering Topological Materials

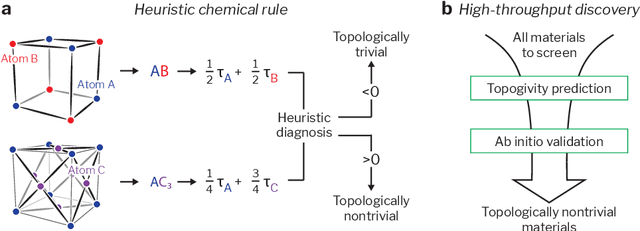
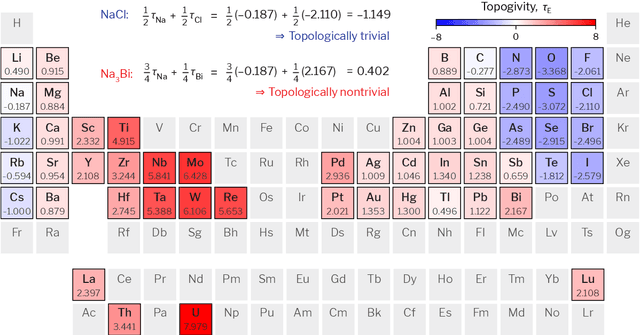
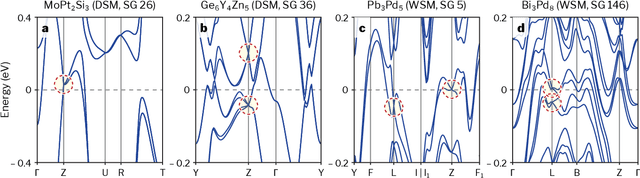
Topological materials present unconventional electronic properties that make them attractive for both basic science and next-generation technological applications. The majority of currently-known topological materials have been discovered using methods that involve symmetry-based analysis of the quantum wavefunction. Here we use machine learning to develop a simple-to-use heuristic chemical rule that diagnoses with a high accuracy whether a material is topological using only its chemical formula. This heuristic rule is based on a notion that we term topogivity, a machine-learned numerical value for each element that loosely captures its tendency to form topological materials. We next implement a high-throughput strategy for discovering topological materials based on the heuristic topogivity-rule prediction followed by ab initio validation. This way, we discover new topological materials that are not diagnosable using symmetry indicators, including several that may be promising for experimental observation.